Giả sử phương trình (1) được đưa về dạng tương đương :
x = g(x) 2)
từ giá trị xo nào đó gọi là giá trị lặp đầu tiên ta lập dãy xấp xỉ bằng công thức:
xn= g(x+-1) (3)
với n = 1,2,....
Hàm g(x) được gọi là hàm lặp. Nếu dãy xn ® a khi n ®µ thì ta nói phép lặp (3) hội tụ.
Ta có định lí: Xét phương pháp lặp (3), giả sử :
- [a,b] là khoảng phân li nghiệm a của phương trình (1) tức là của (2)
- mọi xntính theo (3) đều thuộc [a, b]
trong đó q là một hằng số thì phương pháp lặp (3) hội tụ
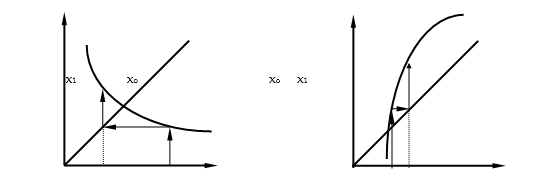
Ta có thể minh hoạ phép lặp trên bằng hình vẽ trên.
Cách đưa phương trình f(x) = 0 về dạng x = g(x) được thực hiện như sau: ta thấy f(x) = 0 có thể biến đổi thành x = x + lf(x) với l ¹ 0. Sau đó đặt x+lf(x) = g(x) sao cho điều kiện (4) được thoả mãn.
Ví dụ: xét phương trình
x3+ x - 1000 = 0
Sau bước giải sơ bộ ta có nghiệm x1Î ( 9,10 )
Nếu đưa phương trình về dạng:
x = 1000 - x3 = g(x)
thì dễ thấy | g'(x) | > 1 trong khoảng ( 9, 10 ) nên không thoả mãn điều kiện (4)
Chúng ta đưa phương trình về dạng
thì ta thấy điều kiện (4) được thoả mãn.Xây dựng dãy xấp xỉ
với xo chọn bất kì trong ( 9, 10 )
Trên cơ sở phương pháp này chúng ta có các chương trình tính toán sau:
Chương trình giải phương trình exp((1/3)*ln(1000-x)) với số lần lặp cho trước
Chương trình 2-1
//lap don
#include <conio.h>
#include <stdio.h>
#include <math.h>
void main()
{
int i,n;
float x,x0;
float f(float);
clrscr();
printf("Cho so lan lap n = ");
scanf("%d",&n);
printf("Cho gia tri ban dau cua nghiem x0 = ");
scanf("%f",&x0);
x=x0;
for (i=1;i<=n;i++)
x=f(x);
printf("Nghiem cua phuong trinh la :%.4f",x);
getch();
}
float f(float x)
{
float a=exp((1./3.)*log(1000-x));
return(a);
}
và chương trình giải bài toán bằng phương pháp lặp với sai số cho trước
Chương trình 2-2
//lap don
#include <conio.h>
#include <stdio.h>
#include <math.h>
void main()
{
int i;
float epsi,x,x0,y;
float f(float);
clrscr();
printf("Cho sai so epsilon = ");
scanf("%f",&epsi);
printf("Cho gia tri ban dau cua nghiem x0 = ");
scanf("%f",&x0);
x=x0;
y=f(x);
if (abs(y-x)>epsi)
{
x=y;
y=f(x);
}
printf("Nghiem cua phuong trinh la %.6f",y);
getch();
}
float f(float x)
{
float a=exp((1./3.)*log(1000-x));
return(a);
}
Cho giá trị đầu xo = 1.Kết quả tính toán x = 9.966555









Không có nhận xét nào:
Đăng nhận xét